Finding Intersection Point(s) of Two Circles

收藏到CSDN网摘

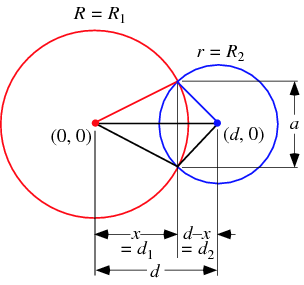
This is a very common problem of finding the intersection point(s) of two circles. Visually, it is easy to define the three cases: no intersection, touching (single intersection point), and two intersection points. Analytically, mathematical calculations are required to work out the exact intersection position(s) (if any) by using the equations of the two circles. A more detailed explanation could be find from HERE and HERE.


Below, it's my implementation in Matlab. The inputs are c1 and c2, which are both vectors representing a circle in the format of [x,y,d]. The output is the point list matrix sorted using y coordinates. If there is no intersection, it is an empty matrix. For touching case, it is a single-row matrix (or vector) in the format of [x,y]. Otherwise, it is a 2*2 matrix forming by the coordinates of the two intersection points: [x1,y1;x2,y2].

%% get intersection point of two circles
% reference:
% http://2000clicks.com/mathhelp/GeometryConicSectionCircleIntersection.aspx
% c1, c2 are given in the format of [x,y,d]
% pts is the intersection point or empty matrix
% Note: pts is sorted by y coordinates
function pts = get_intersect_point(c1,c2)
pts = [];
% two centres
xa = c1(1);
ya = c1(2);
ra = c1(3)/2;
xb = c2(1);
yb = c2(2);
rb = c2(3)/2;
% dist square
d2 = (xb-xa)^2+(yb-ya)^2;
% radii sum square
sumr2 = (ra+rb)^2;
% k is the area of triangle formed by the centers of the two circles and one of 
% their points of intersection (see reference)
k = ((sumr2-d2)*(d2-(ra-rb)^2))^0.5/4;

% no intersection
if d2>sumr2
return;
end
% assume 2 intersection points
x1 = (xb+xa)/2+(xb-xa)*(ra*ra-rb*rb)/d2/2+2*(yb-ya)*k/d2;
y1 = (yb+ya)/2+(yb-ya)*(ra*ra-rb*rb)/d2/2-2*(xb-xa)*k/d2;
x2 = (xb+xa)/2+(xb-xa)*(ra*ra-rb*rb)/d2/2-2*(yb-ya)*k/d2;
y2 = (yb+ya)/2+(yb-ya)*(ra*ra-rb*rb)/d2/2+2*(xb-xa)*k/d2;
pts = [x1,y1;x2,y2];
% check if there is only 1 point
pts = unique(pts,'rows');
% sort by y coordinates
pts = sortrows(pts,2);

end

Matlab has a built-in function circcirc for the same purpose. But the return values are two vectors for x and y respectively.

Similarly, line-circle intersection could be calculated by another function linecirc.