Tetrahedron Properties

收藏到CSDN网摘

做CFD与FEA分析,经常要与网格打交道.而FEA分析最常用的网格大概就数四面体网格了(tetrahedron).无论是4-node还是10-node,其几何形状都是经典的三棱锥.本文记录一些用到的四面体属性知识.


三维空间的四面体(三棱锥)可与二维空间的三角形互相联系起来,很多属性都可以一一对应过来.例如内心,外心等等.其中外接球由于过四面体四个顶点,是该四面的最小包围体,有时非常有用.外接球(circumscribed sphere)可由外接球心与半径规定.根据其过四个顶点的性质,可以解方程组求解.下面的代码是使用克莱姆法则求解外接球心.一旦球心坐标求出,与任意顶点的距离就是半径.具体分析过程可见这里.如果需要检测计算结果是否正确,这里可以在线测试.

// using four points to calculate circumscribed sphere center
// note: Cramer's rule
// https://stackoverflow.com/questions/13600739/calculate-centre-of-sphere-whose-surface-contains-4-points-c
// http://mathworld.wolfram.com/Circumsphere.html
// for checking: http://www.convertalot.com/sphere_solver.html
void Tet3d::calCC(void)
{
 const double x1 = p1.x;
 const double y1 = p1.y;
 const double z1 = p1.z;
 const double x2 = p2.x;
 const double y2 = p2.y;
 const double z2 = p2.z;
 const double x3 = p3.x;
 const double y3 = p3.y;
 const double z3 = p3.z;
 const double x4 = p4.x;
 const double y4 = p4.y;
 const double z4 = p4.z;
 double a11, a12, a13, a21, a22, a23, a31, a32, a33, b1, b2, b3, d, d1, d2, d3;
 a11 = 2 * (x2 - x1); a12 = 2 * (y2 - y1); a13 = 2 * (z2 - z1);
 a21 = 2 * (x3 - x2); a22 = 2 * (y3 - y2); a23 = 2 * (z3 - z2);
 a31 = 2 * (x4 - x3); a32 = 2 * (y4 - y3); a33 = 2 * (z4 - z3);
 b1 = x2*x2 - x1*x1 + y2*y2 - y1*y1 + z2*z2 - z1*z1;
 b2 = x3*x3 - x2*x2 + y3*y3 - y2*y2 + z3*z3 - z2*z2;
 b3 = x4*x4 - x3*x3 + y4*y4 - y3*y3 + z4*z4 - z3*z3;
 d = a11*a22*a33 + a12*a23*a31 + a13*a21*a32 - a11*a23*a32 - a12*a21*a33 - a13*a22*a31;
 d1 = b1*a22*a33 + a12*a23*b3 + a13*b2*a32 - b1*a23*a32 - a12*b2*a33 - a13*a22*b3;
 d2 = a11*b2*a33 + b1*a23*a31 + a13*a21*b3 - a11*a23*b3 - b1*a21*a33 - a13*b2*a31;
 d3 = a11*a22*b3 + a12*b2*a31 + b1*a21*a32 - a11*b2*a32 - a12*a21*b3 - b1*a22*a31;
 this->cc.x = d1 / d;
 this->cc.y = d2 / d;
 this->cc.z = d3 / d;
}

如果你只需要外接球的半径而不关心其球心坐标,也有其他方法,但是需要用到四面体的体积.下面的代码是利用6组棱长与体积来求解外接球半径.当所有顶点坐标已知,棱长很容易求解.具体公式见这里.

// using 6 edges to calcualte circumscribed sphere radius
// note: https://en.wikipedia.org/wiki/Tetrahedron#Circumradius
// edge: 12,13,14,23,24,34
void Tet3d::calRC(void)
{
 double a, b, c, A, B, C, V;
 if (this->edges[0] < 0) this->calEdges();
 a = this->edges[0];
 b = this->edges[1];
 c = this->edges[2];
 A = this->edges[5];
 B = this->edges[4];
 C = this->edges[3];
 if (this->vol < 0) this->calVol();
 V = this->vol;
 this->rc = (double)sqrt((a*A+b*B+c*C)*(a*A+b*B-c*C)*(a*A-b*B+c*C)*(-a*A+b*B+c*C)) / 24 / V;
}

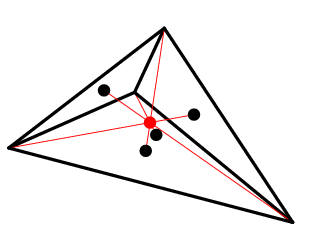
上面直接求解外接球半径的代码涉及四面体体积的计算,而四面的体积则是一个非常重要的性质.可以用来计算四面体内部任意点的插值坐标.几何解释见这里,利用判断的点P替换原四面体顶点P1-P4,来计算分割形成的小四面体的体积V1-V4,那么四个插值坐标就是Vi/V,但是必须先判断以确定点P是否在四面体内部.

判断P是否在内部也有多种办法,因为上面计算小四面体体积的过程可用下面的代码来计算.四面体四个顶点形成的矩阵的行列式(注意,这是个有符号量,四面体的体积等于abs(Det4(P1,P2,P3,P4))/6).如果原四面体的行列式值记为D0,用点P分别替换P1-P4,得到新的行列式至记为D1-D4(Di表示P替换了Pi).那么:

1.如果任意Di与D符号相反,则P在四面体外部.
2.如果任意Di==0,那么P在除Pi外的三点确定的平面上(有时可能在棱上,这时会有两个Di==0)
3.如果所有Di都与D同号,那么插值坐标为Di/D.

注:可以在计算前分别计算P到顶点的距离,如果任意距离==0,那么可以直接写插值坐标对应分量是1,其余为0.

具体分析见这里.

// calculate determinant of 4*4 matrix
///************************************************************************
/// @fn   Det4
/// @brief  calculate the determinate of a 4*4 matrix
// 
// Note: http://steve.hollasch.net/cgindex/geometry/ptintet.html
// | x1 y1 z1 1 |
// | x2 y2 z2 1 |
// | x3 y3 z3 1 |
// | x4 y4 z4 1 |
///************************************************************************
double Det4(Point3d &p1, Point3d &p2, Point3d &p3, Point3d &p4)
{
 const double x1 = p1.x;
 const double x2 = p2.x;
 const double x3 = p3.x;
 const double x4 = p4.x;
 const double y1 = p1.y;
 const double y2 = p2.y;
 const double y3 = p3.y;
 const double y4 = p4.y;
 const double z1 = p1.z;
 const double z2 = p2.z;
 const double z3 = p3.z;
 const double z4 = p4.z;
 return (x1*(y2*z3 + y4*z2 + y3*z4 - y3*z2 - y2*z4 - y4*z3)
  - x2*(y1*z3 + y4*z1 + y3*z4 - y3*z1 - y1*z4 - y4*z3)
  + x3*(y1*z2 + y4*z1 + y2*z4 - y2*z1 - y1*z4 - y4*z2)
  - x4*(y1*z2 + y2*z3 + y3*z1 - y2*z1 - y3*z2 - y1*z3));
}

最后,也是最经典最简洁的四面体体积,在向量空间非常好理解.如果取任意点(例如P1)为原点,然后计算从P1出发的三条棱分别记为V12=a,V13=b,V14=c.这里abc都是矢量.那么四面体的体积V=|a.(b*c)|/6.语言描述就是"向量a点乘向量b与向量c的叉积的结果的绝对值除以6".而这个特殊的"点乘叉乘"三向量的运算过程在线性代数中被称为三向量的混合积.那么,四面体的体积也可以用几何意义来计算(但是需要针对Vec3d重载运算符-和*来做减法和叉积):

// scalar triple product: v = |a.(b*c)|/6
void Tet3d::calVol(void)
{
 Vec3d v12 = p2 - p1;
 Vec3d v13 = p3 - p1;
 Vec3d v14 = p4 - p1;
 this->vol = fabs(v12.dot(v13*v14)) / 6;
}

在学习的过程中也顺便复习了一下立体几何的相关知识,三维点P到平面(n,d)的距离可以用P.n+d来计算(注意虽然P是点的坐标,但是同时它的三个分量也可以看作是从原点O指向点P的向量OP,n是一个向量).式子里面的P.n就是向量点积,相当于向量OP向平面的法向量投影,然后加上d,d是原点到平面的距离(这里说的距离都是有符号量).下面的代码可以计算一个点到三个不共线的点确定的平面的距离.这里有详细的计算过程和几何解释.

// *****************************************************************************
//  Plane3d CLASS: ax+by+cz+d = 0 or a(x-x1)+b(y-y1)+c(z-z1) = 0
// *****************************************************************************
class Plane3d
{
public:
 Point3d p1;
 Point3d p2;
 Point3d p3;
 Vec3d dir; // unit vector of the normal direction

 Plane3d(void) :p1(Point3d()), p2(Point3d()), p3(Point3d()) {}
 Plane3d(const Point3d &_p1, const Point3d &_p2, const Point3d &_p3)
 {
  p1.x = _p1.x; p1.y = _p1.y; p1.z = _p1.z;
  p2.x = _p2.x; p2.y = _p2.y; p2.z = _p2.z;
  p3.x = _p3.x; p3.y = _p3.y; p3.z = _p3.z;
  dir = ((p2 - p1)*(p3 - p1)).norm();
 }
 Plane3d(const Plane3d &p) : Plane3d(p.p1, p.p2, p.p3) {}

 // signed distance to a plane from a given point
 // https://mathinsight.org/distance_point_plane
 double dist(Point3d &p) { return ((p - p1).dot(dir)); }
};